Bowen's Tech Blog

Summary for some exercise.

Elements of OO

3 elements of object oriented: Inheritance, encapsulation, and polymorphisn. Interface is another important element of the OOP.

Inheritance

Categories

Inherit is way to describe the relationship between between classes. If class A IS-A class B, we call class A Subclass or Derived class, call class B as Parent class or Base Class or Super Class.

Subclass could inherit the properties and methods from parent class, and subclass could also add or modify new properties and methods.

In .NET, it cloud be divided into 2 categories:

• Inherit a class
  • Can only inherit one class at one time
  • The top parent class for any class in .NET is System.Object
  • System.Object has 4 functions: ToString, Equals, GetHashCode, Finalize.
• Inherit an interface
  • Can inherit several interfaces at one time
  • Can divide the objects (class) and actions (interface) during the inherit

Modify existing classes - Adapter Design Patterns

Adapter pattern is a way to modify the existing classes to meet the new requirements. It has two categories:

• Adapter pattern of class
  • Design a new subclass which inherits previous classes and the new interface
• Adapter pattern of object
  • Design a new subclass which inherits the new interface and get the parameter of previous base class

Additional Knowledge - Abstract Class

• Abstract class
  • The class can only be inherited but cannot be instantiated.
  • All abstract methods in the abstract class need to be override in subclass.
• Abstract function v.s. Virtual functions
  • Abstract function doesn’t have the function body, and it requires to be override in the subclass.
  • Virtual function could have the function body, and it could be override or not in the subclass.

Encapsulation

It is for class to hide some private field or methods but leave public interface for other classes. The rules include

• Field
  • Declare field (variables of class) as private
• Property
  • Declare property as public
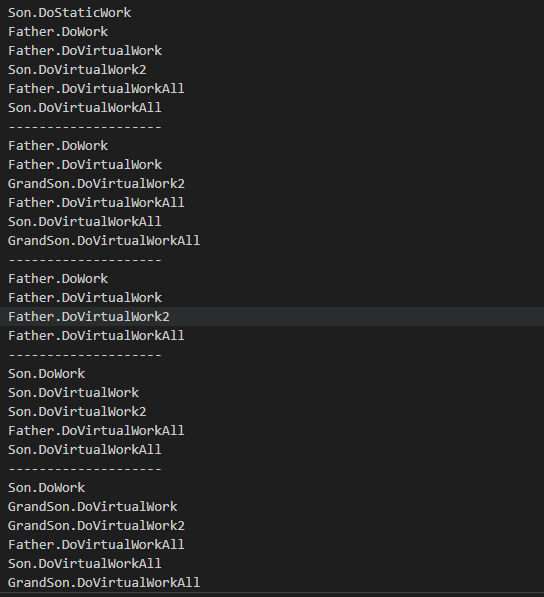
  • supporting get and/or set
  • Use property instead of field directly
  • Property is transferred to function during the compile
• Functions
  • Functions that other classes need to call can be declared as public; other functions of classes should be declared as private

Polymorphisn

This allows users to set a base class reference points to different subclass. When call the methods in base class, the same method acts differently according to the implement in subclass. The specific relationship between reference and real methods will be determined after the compile.

We can declare a base class variable / interface but still points to the subclass object. Assume the base class is A, and the subclass is B. When we call a method in A, the compiler will check whether this method was declared virtual.

• If it is not declared virtual, call this method directly.
• If it is declared virtual, then will check whether subclass B has override this method
  • If there is a override method, call this method
  • If there is not override method, recursively check the parent class whether override this method

Interface

• Interface usually ends with able, which shows a kind of ability of the class, also described a can-do.
• Interface is like a class containing abstract methods. The methods inside interface are declared public abstract automatically.
• Methods in interface need to be implemented in the subclass, but no need to use abstract, virtual, override keywords.
• Interface only contains the single category of functions.
• When create a new object, we can declare the pointer as the interface but points to object inherited from the interface.

See here for more info.

Design Principles of OO

The final design principles of OO is Abstract-oriented, loosely coupled.

Single Responsibility Principle

One class only do one thing, and only change due to one reason.

For example, an interface defines the basic actions and class A inherit the interface and implement those actions. Class B adds some judging methods and it also inherits the interface and include a field inheriting from the interface (an object of class A), so class B just call A’s functions instead of implement them.

Open Closed Principle

Open for extension, closed for modifying. Program for abstract instead of specific.

For example, if there will be much similar methods, we can put them into different classes but inherits a same interface. Then we use another manager class to create an interface reference for different classes. When a new method adds into the system, we can just implement the new class inheriting from the interface.

Dependency Inversion Principle

Depends on abstract. Classes should depend on interface rather than other classes.

Some principle:

• Less inheritance, more aggregate
• One-way dependency (Low coupling, high cohesion)
• Encapsulation abstraction
• Dependence should ends on abstract class or interface

For example, use interface pointer to call method. Since different object implement different methods, the method will automatically link to the right method according to the type of created object. When new kinds of methods add, just implement new classes inherited from the interface and previous code don’t need to change.

In other words, we solve the problem of deciding what versions of the similar method to use by the Polymorphisn(different methods have a same interface) rather than write judging code.

Interface Segregation Principle

Use many small interface instead of a big interface.

Class could inherit several interfaces that are useful to the class.

Liskov Substitution Principle

Subclass must be able to replace base class.

Subclass must have all the methods of base class. The base class should declare the method virtual and subclass override that method. This can reduce the unnecessary judging code.

Composite/Aggregate Reuse Principle

Reduce coupling between classes by aggregating existing classes/interface instead of inheriting objects.

One example is the adapter pattern, which is a way to modify the existing classes to meet the new requirements. It has two categories:

• Adapter pattern of class
  • Design a new subclass which inherits previous classes and the new interface
  • Requires to inherit a class, will increasing the coupling between classes
• Adapter pattern of object
  • Design a new subclass which inherits the new interface and contains a field which is the base class of classes that need to be extended
  • Use aggregate (combine class and interface together), reduce coupling

Design Pattern of OO

Dependency / coupling

Kinds of coupling

• Non-coupling: two classes are independent
• Concrete coupling: one class have the reference of another class
• Abstract coupling: one class have the reference of another abstract class, which can achieve the Polymorphisn

Reasons causing the coupling

• Inheritance
• Aggregation
• Interface
• Call methods or reference
• Call services

Design principle to reduce the coupling

• Dependency Inversion Principle (DIP)
  • Add a middle class
  • Let class use the reference of the interface which another class inherits from, instead of use the reference of another class
• Inversion of Control (IoC)
  • Let the system control the code
• Dependency Injection (DI)
  • Interface Injection (Use the parameters of methods of method)
  • Constructor Injection (Use constructor method)
  • Setter Injection (Properties)

Design Pattern to reduce the coupling happening in when need to create(new) an object

• Factory Mode
  • Use interface and generic
• Dependency Injection
  • Use Unity container to create new object
  • Use the resolve method of Unity container to dynamically create different objects inherited from the same abstract class or interface

Design Pattern

| Category | Name | Function |
| — | — |
| Creation Pattern | Factory Method Pattern | A dynamic way to deal with the process when create a new object, especially for creating different objects but those objects have same base class or interface |
| | Singleton Pattern | One class only have one instance |
| Structural model | Bridge Pattern | Divide the implement with the logic |
| | Proxy Pattern | Encapsulation the complex logic, use proxy to control the the create and call the original object |
| | Adapter Pattern | Don’t change previous classes, add new interfaces |
| | Composite Pattern | Use the same method to process all objects in a composite |
| | Decorator Pattern | Dynamically add or remove status or actions |
| | Facade Pattern | Divide the logic layer and the presentation layer |
| Behavioral model | Template Method Pattern | Define the template in base class and implement them in subclass |
| | Iterator Pattern | Provide a method to get every element in a container but not exposure to outside |
| | Chain of Responsibility Pattern | Form the methods a linked list,traverse the linked list and get the right method |
| | Command Pattern | Encapsulation the request as a class, divide the execution of order and duty |
| | Observer Pattern | one v.s. many. One object’s status changes, other objects will get the event, then they will change. e.g. the delegate and event in C# |
| | Strategy Pattern | Encapsulation the part changing a lot as interface |

Object-Oriented & Object-Based

Object-Based: Handle the object with field and method, but the object doesn’t inherit any class, thus no Polymorphisn.

.NET Closure

Closure is the body formed by methods and environment attached to the method. It can allow several methods operate the same element.

Good Code

• Good Name
  • Pascal Casing for namespace, class, interface, method, event, enum
  • Camel Casing for paramenters, private members
  • Attribute, delegate, exception as the suffix
• Security of thread

Reference

1. 《你必须知道的.NET（第二版）》，第1部分，王涛著

恭喜宝贝儿拿到微软的奥佛！！！！！
牛逼！！！！！

This post talks about the knowledge (grammar, concepts) of C++.

Templates for efficient programming.

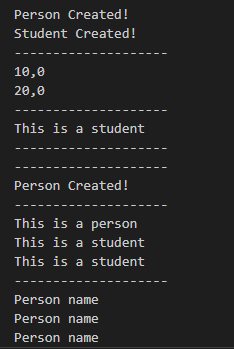
Inheritance is a very important feature in C#. It can allow you to achieve the polymorphisn, which is very very important feature which could help you to write the code in a good design (easy to extend).

Category

• Inherit a class
  • Inherit a abstract class
    • Must implement the abstract methods in the abstract class
    • Can override/new the virtual methods in the abstract class
  • Inherit a normal class
    • Can override/new the virtual methods in the abstract class
• Inherit an interface
  • Must implement all members (properties, methods, events) in the interface.

The different field

When class Student inherits class Person publicly. Those functions and members which are public and protected in class Person can be used in class Student. Functions and members which are private in class Person cannot be used in class Student.

However, if there is a public/protected function in class Person, which uses the private members of class Person. When class Student call that functions, those private members in class Person could also be used via this function.

Base function

Use base.function() in the class Student can call the functions implemented in class Person (the functions should be public/protected). This is often used when class Student rewrite the methods of class Person but still need to call the method of class Person.

About override/new keyword

Polymorphisn often happens when you declare a class Person reference, but you point it to an object instantiated from class Student.

When there is a abstract/virtual method in class Person, class Student could use override/new to rewrite that method. At this moment, call the which are rewrote can lead to charming results.

Since the abstract class can’t be instantiated, we just talked about those virtual - override/new relationship.

• If the reference type and the object type is the same. Call those functions are calling the function in their own field.
• If the reference type is the base class and the object type is the subclass.
  • If the method is declared override in subclass. Call this method from the reference is executing the method in subclass.
  • If the method is declared new in subclass. Call this method from the reference is executing the method in base class.

If the method is declared abstract in base class. You cannot call it except the subclass override this method.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78

using System;

namespace testInherit
{
    class Person
    {
        protected int age = 10;
        protected int id = 0;
        public Person()
        {
            Console.WriteLine("Person Created!");
        }
        public void ShowBaseInfo()
        {
            Console.WriteLine(age.ToString() + ","+ id.ToString());
        }

        public virtual void ShowType()
        {
            Console.WriteLine("This is a person");
        }

        public virtual void ShowName()
        {
            Console.WriteLine("Person name");
        }
    }

    class Student : Person
    {
        new int age = 20;
        public Student()
        {
            Console.WriteLine("Student Created!");
        }
        public void ShowInfo()
        {
            Console.WriteLine(age.ToString() + ","+ id.ToString());
        }

        public override void ShowType()
        {
            Console.WriteLine("This is a student");
        }

        public new void ShowName()
        {
            Console.WriteLine("Person name");
        }
    }

    class Program
    {
        static void Main(string[] args)
        {
            Student student = new Student();
            
            Console.WriteLine("--------------------");
            student.ShowBaseInfo();
            student.ShowInfo();
            Console.WriteLine("--------------------");
            student.ShowType();
            Console.WriteLine("--------------------");
            Console.WriteLine("--------------------");

            Person person = new Person();
            Person person_student = student;
            Console.WriteLine("--------------------");
            person.ShowType();
            person_student.ShowType();
            student.ShowType();
            Console.WriteLine("--------------------");
            person.ShowName();
            person_student.ShowName();
            student.ShowName();
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127

using System;

namespace TestCSharp
{
    public class Father
    {
        public static void DoStaticWork()
        {
            Console.WriteLine("Father.DoStaticWork");
        }

        public void DoWork()
        {
            Console.WriteLine("Father.DoWork");
        }

        public virtual void DoVirtualWork()
        {
            Console.WriteLine("Father.DoVirtualWork");
        }

        public virtual void DoVirtualWork2()
        {
            Console.WriteLine("Father.DoVirtualWork2");
        }

        public virtual void DoVirtualWorkAll()
        {
            Console.WriteLine("Father.DoVirtualWorkAll");
        }
    }

    public class Son : Father
    {
        public static void DoStaticWork()
        {
            Console.WriteLine("Son.DoStaticWork");
        }
        public void DoWork()
        {
            Console.WriteLine("Son.DoWork");
        }

        public new virtual void DoVirtualWork()
        {
            Console.WriteLine("Son.DoVirtualWork");
        }

        public override void DoVirtualWork2()
        {
            Console.WriteLine("Son.DoVirtualWork2");
        }
        public override void DoVirtualWorkAll()
        {
            base.DoVirtualWorkAll();
            Console.WriteLine("Son.DoVirtualWorkAll");
        }
    }

    public class Grandson : Son
    {
        public override void DoVirtualWork()
        {
            Console.WriteLine("GrandSon.DoVirtualWork");
        }

        public override void DoVirtualWork2()
        {
            Console.WriteLine("GrandSon.DoVirtualWork2");
        }
        public override void DoVirtualWorkAll()
        {
            base.DoVirtualWorkAll();
            Console.WriteLine("GrandSon.DoVirtualWorkAll");
        }
    }

    class Program
    {
        static void Main(string[] args)
        {
            Father son = new Son();
            Son.DoStaticWork();
        
            son.DoWork();
            son.DoVirtualWork();
            son.DoVirtualWork2();
            son.DoVirtualWorkAll();

            Console.WriteLine("--------------------");

            Father gson = new Grandson();

            gson.DoWork();
            gson.DoVirtualWork();
            gson.DoVirtualWork2();
            gson.DoVirtualWorkAll();

            Console.WriteLine("--------------------");

            Father father = new Father();

            father.DoWork();
            father.DoVirtualWork();
            father.DoVirtualWork2();
            father.DoVirtualWorkAll();

            Console.WriteLine("--------------------");

            Son realSon = new Son();

            realSon.DoWork();
            realSon.DoVirtualWork();
            realSon.DoVirtualWork2();
            realSon.DoVirtualWorkAll();

            Console.WriteLine("--------------------");

            Son realgSon = new Grandson();

            realgSon.DoWork();
            realgSon.DoVirtualWork();
            realgSon.DoVirtualWork2();
            realgSon.DoVirtualWorkAll();
        }
    }
}

Reference

Asynchronous method is implemented in C# by using async/await keywords.

Async/Await keywords

That’s the goal of asynchronous: enable code that reads/writes like a sequence of statements, but executes in a much more complicated order based on external resource allocation and when tasks complete.

Without language support, writing asynchronous code required callbacks, completion events, or other means that obscured the original intent of the code. In C#, keywords async and await are used to achieved a asynchronous program. The function return immediately when it meets a await. A code sample is like following.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

using System;
using System.Threading.Tasks;


namespace TestAsyncIL
{
    class TestAsync
    {
        public async void Method1()
        {
            Console.WriteLine("Start Method 1");
            for (int i = 0; i < 3; i++)
            {
                await Task.Delay(330);
                Console.WriteLine("Method 1: " + i.ToString());
            }
        }

        public async void Method2()
        {
            Console.WriteLine("Start Method 2");
            for (int i = 0; i < 3; i++)
            {
                await Task.Delay(330);
                Console.WriteLine("Method 2: " + i.ToString());
            }
        }

        public void Method3()
        {
            Console.WriteLine("Start Method 3");
            for (int i = 0; i < 3; i++)
            {
                Console.WriteLine("Method 3: " + i.ToString());
            }
        }
    }

    class Program
    {
        static void Main(string[] args)
        {
            TestAsync testAsync = new TestAsync();
            testAsync.Method1();
            testAsync.Method2();
            testAsync.Method3();
            Console.Read();
            /* Output is (replaced '\n' by ',')
            Start Method 1, Start Method 2, Start Method 3
            Method 3: 0, Method 3: 1, Method 3: 2
            Method 1: 0, Method 2: 0, Method 1: 1
            Method 2: 1, Method 1: 2, Method 2: 2
            */
        }
    }
}

How to code executed:

1. Run Method1, code output method1, then encounter await, get back to the main function
2. Run Method2, code output method2, then encounter await, get back to the main function
3. Run Method3, since the running time is less than 330 milliseconds, it will output all the content in Method3
4. After 330 milliseconds from Method1 returning, Method1 output the next str
5. After 330 milliseconds from Method2 returning, Method2 output the next str
6. Repeat 4 and 5 until output all string.

Note. the step 4 and 5 won’t output if we don’t add the ReadKey method in the end because the main thread will ends and those asnyc methods still in the same thread thus end, too.

Analysis of metadata

In IL, we find that the compiler generate 2 classes for Method1 and Method2 called <Method1>d__0 and <Method2>d__1. The two classes are state machines, the implement the interface TStateMachine. The class contains the following elements.

• Fields
  • int state
  • TestAsync this
  • AsyncVoidMethodBuilder builder
  • TaskAwaiter u__1
  • int 5__1 (the local int i in for loop)
• Methods
  • .ctor
  • MoveNext
  • SetStateMachine

There are two important data types. System.Runtime.CompilerServices.AsyncVoidMethodBuilder and System.Runtime.CompilerServices.TaskAwaiter

• AsyncVoidMethodBuilder
  • A struct, value type
  • Represents a builder for asynchronous methods that do not return a value.
  • Its Create method will return a instance of the builder
  • Its Start<TStateMachine> method will begin running the builder with the associated state machine
• TaskAwaiter
  • A struct, value type
  • Provides an object that can check whether current asynchronous task is completed and waits for the completion of an asynchronous task
  • Properties
    • IsCompleted. Gets a value that indicates whether the asynchronous task has completed.
  • Methods
    • GetResult. Ends the wait for the completion of the asynchronous task.
    • OnCompleted(Action). Sets the action to perform when the TaskAwaiter object stops waiting for the asynchronous task to complete.
    • UnsafeOnCompleted(Action). Schedules the continuation action for the asynchronous task that is associated with this awaiter.

IL execution pipeline

For the Method2 itself, the IL code is as follows

Once we call the Method2, it does the following things.

1. Initializes a class called <Method2>d__1.
2. Assign the current instance to <Method2>d__1::this
3. Call AsyncVoidMethodBuilder::Create<<Method2>d__1> to create a async void instance for the state machine
4. Set <Method2>d__1::state to -1
5. Call AsyncVoidMethodBuilder.Start, the passing state machine is the class <Method2>d__1
6. Call the <Method2>d__1::MoveNext, since the state is -1, output the str, and change state to 0
7. Once the state is set to 0, initialize the 5__1 field as 0, then call the Task.Delay method, and get awaiter for this task and set it to u__1 field
8. Check u__1::IsCompleted. If haven’t finish, call AsyncVoidMethodBuilder::AwaitUnsafeOnCompleted<5__1, <Method2>d__1>, which will call <Method2>d__1::MoveNext method when the status of the awaiter is complete
   • Note. I think the AsyncVoidMethodBuilder will set the <Method2>d__1::MoveNext to 5__1::UnsafeOnCompleted(Action)
9. The next time it call the MoveNext method, the code will execute different logic since the state has been changed.

Asynchronous method return types

Async methods can have the following return types

| void | Task | Task<TResult>
—–|——|——|—————
has return statement | No | Yes | Yes
return statement type | - | Task | Task<TResult>
can assign to delegate or event | Yes | Yes | Yes
can assign to Task | No | Yes | Yes
caller can know whether this method has completed (create a awaiter for it) | No | Yes | Yes
its awaiter has return statement | - | No | Yes
its awaiter return type | - | - | TResult

Task and Task class

Compared to execute a thread to do actions, the Task class is used to execute asynchronously, and it can track the status of this asynchronous action, including whether it finish and what is the return value. Most commonly, a lambda expression is used to specify the work that the task is to perform.

For operations that return statement, the Task<TResult> class will be used.

Samples

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104

using System;
using System.Threading.Tasks;


namespace TestAsyncIL
{
    struct ReturnArgs
    {
        public int Data { get; set; }
        public string Text { get; set; }
    }

    class TestAsyncTask
    {
        public async Task Method1()
        {
            Console.WriteLine("Start Method 1");
            for (int i = 0; i < 3; i++)
            {
                await Task.Delay(330);
                Console.WriteLine("Method 1: " + i.ToString());
            }
        }

        public async Task<ReturnArgs> Method2()
        {
            Console.WriteLine("Start Method 2");
            for (int i = 0; i < 3; i++)
            {
                await Task.Delay(330);
                Console.WriteLine("Method 2: " + i.ToString());
            }
            return new ReturnArgs() { Data = 2, Text = "Task Finished!" };
        }

        public void Method3()
        {
            Console.WriteLine("Start Method 3");
            for (int i = 0; i < 3; i++)
            {
                Console.WriteLine("Method 3: " + i.ToString());
            }
        }
    }

    class Program
    {
        static void Main(string[] args)
        {
            // mMain1();
            // mMain2();
            mMain3();
            Console.ReadKey();
        }

        static async void mMain1()
        {
            TestAsyncTask testAsync = new TestAsyncTask();
            testAsync.Method1();
            testAsync.Method2();
            testAsync.Method3();
            /* Output is (replaced '\n' by ',')
            Start Method 1, Start Method 2, Start Method 3
            Method 3: 0, Method 3: 1, Method 3: 2
            Method 1: 0, Method 2: 0, Method 1: 1
            Method 2: 1, Method 1: 2, Method 2: 2
            */
        }

        static async void mMain2()
        {
            TestAsyncTask testAsync = new TestAsyncTask();
            await testAsync.Method1();
            ReturnArgs args = await testAsync.Method2();
            Console.WriteLine(args.Data.ToString() + " " + args.Text);
            testAsync.Method3();
            /* Output is (replaced '\n' by ',')
            Start Method 1, Method 1: 0, Method 1: 1, Method 1: 2
            Start Method 2, Method 2: 0, Method 2: 1, Method 2: 2
            2 Task Finished!
            Start Method 3, Method 3: 0, Method 3: 1, Method 3: 2
            */
        }

        static async void mMain3()
        {
            TestAsyncTask testAsync = new TestAsyncTask();
            Task a = testAsync.Method1();
            Task<ReturnArgs> b = testAsync.Method2();
            Task.WaitAny(a);
            var args = await b;
            Console.WriteLine(args.Data.ToString() + " " + args.Text);
            testAsync.Method3();
            /* Output is (replaced '\n' by ',')
            Start Method 1, Start Method 2
            Method 1: 0, Method 2: 0, 
            Method 1: 1, Method 2: 1,
            Method 1: 2, Method 2: 2,
            2 Task Finished!
            Start Method 3, Method 3: 0, Method 3: 1, Method 3: 2
            */
        }
    }
}

In the mMain1 method, the Method1 and Method2 are still be executed in a synchronously. So the output is the same with the void-returning async method.

In the mMain2 method, we create the awaiter for the Method1 and Method2, so Method2 will be called after Method1, and Method3 will be called after Method2.

In the mMain3 method, we firstly run the Method1 and Method2 synchronously and assign them to Task and Task<TResult> variables. So the two methods will run at the same time. Then we use Task.WaitAny and create a awaiter for Method2, so Method3 will run after Method1 and Method2.

Analysis in IL

Similarly, the complier will generate 2 state machine classes for Method1 and Method2 and 3 state machine for mMain1, mMain2, mMain3.

In the state machine of Method1 and Method2, it is similar to the void-returning async method but it uses AsyncTaskMethodBuilder<TResult> classes to build the async task. In Method2, when it is finished, it uses SetResult(TResult) method to marks the task as successfully completed and also pass the ReturnArgs statement.

In the mMain2 and mMain3 state machines, there will be TaskAwaiter class and TaskAwaiter<TResult> result. After the awaiter’s property IsCompleted is true, they will call TaskAwaiter<TResult>.GetResult to get the return statement from the AsyncTaskMethodBuilder<TResult>.

Cancellation token to terminate async thread

The Async function can be cancelled by passing a CancellationToken parameter created by a CancellationTokenSource.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

CancellationTokenSource tokenSource;

/// Upload new anchor pipeline
public void UploadNewAnchor()
{
    // Create a new token because token can only by cancelled once
    tokenSource = new CancellationTokenSource();

    // Add the callback methods when the token is cancelled
    tokenSource.Token.Register(() => feedbackBox.text = "Cancel Action!");
    tokenSource.Token.Register(async () =>
    {
        CloudManager.StopSession();
        await cloudManager.ResetSessionAsync();
    });

    // Start the async method
    UploadNewAnchorAsync(tokenSource.Token);
}

/// Upload anchor process, can be canceled anytime
async void UploadNewAnchorAsync(CancellationToken token)
{    
    while (!CloudManager.IsReadyForCreate)
    {
        await Task.Delay(330);
        token.ThrowIfCancellationRequested();
    }

    CloudManager.UploadAnchor();
}

/// Stop the uploading process by the cancellation token
public void StopAction()
{
    if (tokenSource != null)
    {
        tokenSource.Cancel();
        tokenSource.Dispose();
    }
}

Reference

1. AsyncVoidMethodBuilder Struct
2. AsyncTaskMethodBuilder Struct
3. AsyncTaskMethodBuilder Struct
4. TaskAwaiter Struct
5. TaskAwaiter.GetResult Method
6. Task.GetAwaiter Method
7. Task.Delay Method

Description

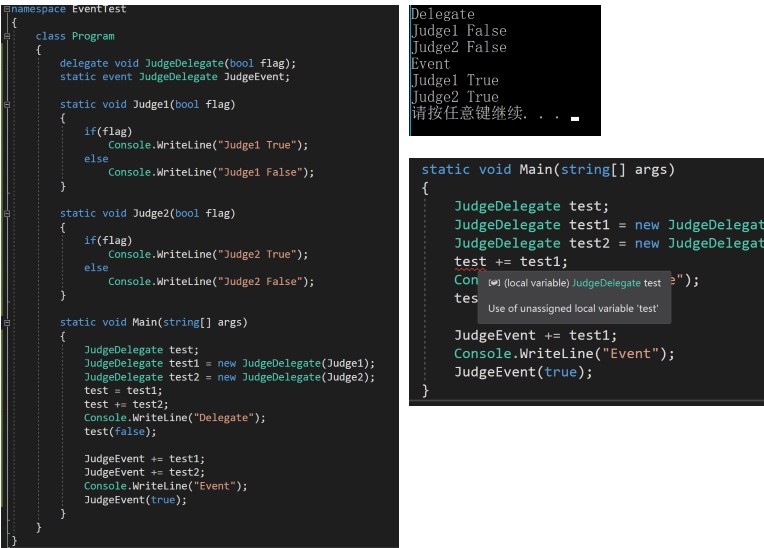
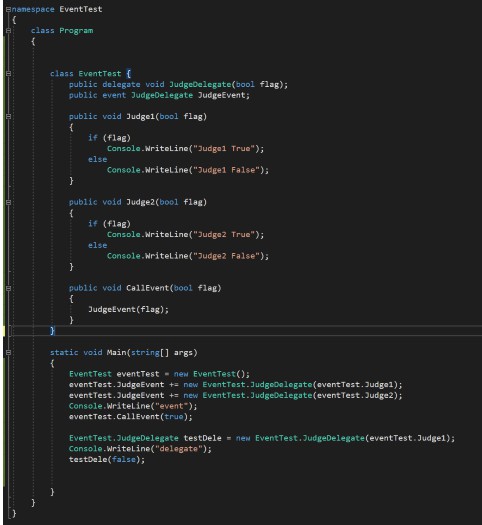
Delegate and event are good ways to “subscribe” some actions to other particular actions carried out by the user or the code. It sounds like function 1 is executed firstly, then function 2, 3, and etc are executed following. Those functions may not in the same class.

For example, they are in class A, class B, class C. If we use the traditional ways to achieve this relationship, we need to call function 2 and 3 in the class A when the function 1 is executed. In this way we will increase the degree of coupling between these classes, that is class A cannot work normally without class B and C.

Therefore, we proposed the ideas of delegate and event. Class B and C could “subscribe” the action publisher in class A with their function 2 and 3. When the action 1 is executed, the class A will call the action publisher, then the class B and C will receive the information that action 1 is executed, so they will execute the action 2 and 3.

Comparison between delegate and event

• Commons
  • They are like the pointer of methods.
  • A method can be used += and -= to be assigned or unassigned to a delegate, and subscribe or unsubscribe the event
  • They both accept anonymous methods (delegate declared, or lambda expression)
  • Event is a specific kind of delegate which will be safer

• Differences

Generic delegate

1
2
3
4
5
6

event EventHandler<bool> OnEvent1;

delegate void MyHandler<T>(int a, T t);
event MyHandler<bool> OnEvent2;        // Generic variable must be set to a fixed type

Func<float, bool> myFuc; 

Delegate declaring anonymous methods

Delegate can be used to declare an anonymous method.

1
2
3
4
5
6
7

event MyHandler<EventArgs> OnTrigger;

OnTrigger += delegate(object sender, EventArgs e)
{
    Console.WriteLine(sender);
    Console.WriteLine(e);
}

See more about anonymous method from here

Execution

The delegate and event can both be used two methods to executed.

• Use myDelegateInstance(paras) or myEvent(paras)
• Use myDelegateInstance.Invoke(paras) or myEvent.Invoke(paras)

They are the same in compiler but the second method could add ? to handle the null conditions.

myDelegateInstance?.Invoke(paras) or myEvent?.Invoke(paras)

Overview

There are several advanced features of C# which are very powerful.

Assembly

An assembly is a collection of types and resources that are built to work together and form a logical unit of functionality. Assemblies are the building blocks of .NET applications. Assemblies has the code that the common language runtime executes.

Assemblies take the 2 forms

• executable (.exe)
  • <compiler command> <module name>
    • csc test.cs
• dynamic link library (.dll) files
  • <compiler command> -t:library <module name>
    • csc -t:library test.cs
  • is similar to a class library that contains types that will be referenced by other assemblies
  • has no entry point to begin execution

Note. Each assembly have only one entry point: DllMain, WinMain, or Main.

• Static assemblies
  • stored on disk in portable executable (PE) files
  • include interfaces, classes, and resources like bitmaps, JPEG files, and other resource files
• Dynamic assemblies
  • run directly from memory and aren’t saved to disk before execution
  • can save dynamic assemblies to disk after they have executed.

To use an assembly in an application, you must add a reference to it. To add a reference to a assembly. Use the following methods

• static Load method of the System.Reflection.Assembly
• GetType method of the Type class can load assemblies
• Load method of the System.AppDomain class
• …

Once an assembly is referenced, all the accessible types, properties, methods, and other members of its namespaces are available to your application as if their code were part of your source file.

Attributes

Attributes can add metadata (information about the types defined in a program) to the program. An attribute is actually an object that is associated with any of these elements: Assembly, Class, Method, Delegate, Enum, Event, Field, Interface, Property and Struct.

The attributes work by placing the name of the attribute enclosed in square brackets ([]) above the declaration of the entity to which it applies. It can contain parameters and the users can customize the attributes.

See here for more info.

In Unity, a public element with the attribute HideInInspector won’t appear in the inspector of Unity Editor. See here for Unity attribute.

A sample of serialization attribute is in the Serialization and Deserialization below.

Exceptions

See here for more info.

Generics

Generics makes it possible to design classes and methods that defer the specification of one or more types until the class or method is declared and instantiated by client code.

A Generics class can also be inherited by other class. The derived class can specify the type of the class or it can inherit without specify the class. Generics class can also add Constrains to give some restrictions of the type.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

using System;
using System.Collections.Generic;

namespace testCSharp
{
    class MyGenericClass<type>
    {
        public type element1;
        public MyGenericClass(type value = default(type))
        {
            element1 = value;
        }
        
        public type function1(type input)
        {
            Console.WriteLine(input);
            return element1;
        }
    }

    class MyDerivedClass1: MyGenericClass<string>
    {
        public MyDerivedClass1(string value)
        {
            element1 = value;
        }
    }
   
    class MyDerivedClass2<type>: MyGenericClass<type> where type: class
    {
        public MyDerivedClass2(type value)
        {
            element1 = value;
        }
    }

    class Program
    {
        static void Main(string[] args)
        {
            MyGenericClass<int> test1 = new MyGenericClass<int>(10);

            int value1 = test1.function1(20);   // 20
            Console.WriteLine(value1);  // 10

            MyGenericClass<string> test2 = new MyGenericClass<string>("abc");

            string value2 = test2.function1("jkl"); //"jkl"
            Console.WriteLine(value2);  //"abc"

            MyDerivedClass1 test3 = new MyDerivedClass1("abc");     
            string value3 = test3.function1("jkl"); //"jkl"
            Console.WriteLine(value3);  //"abc"

            MyDerivedClass2<int> test4 = new MyDerivedClass2<int>("abc");   //complie error, the 'type' must be a reference type
        }
    }
}

See here for more about generic.

Interface

Just define the return type and type of parameters, the specific implementation needs to be finish in derived class, which looks like the header file in C++, that only decare but not implement.

1
2
3
4
5
6
7
8
9
10
11
12

interface IMyInterface
{
    void MethodToImplement();
}

class InterfaceImplementer : IMyInterface
{
    public void MethodToImplement()
    {
        Console.WriteLine("MethodToImplement() called.");
    }
}

See here for more info.

Lambda expression

Lambda expression can be used for anonymous method. The operator => is used.

1
2
3
4
5
6
7
8
9

Func<string> greet = () => "Hello, World!";
Console.WriteLine(greet());

event Handler OnTrigger;
OnTrigger += (sender, e) =>
{
    Console.WriteLine(sender);
    Console.WriteLine(e);
}

Properties

A property is a member that provides a flexible mechanism to read, write, or compute the value of a private field (Member variables or methods in a class or structures). Properties can be used as if they are public data members, but they are actually special methods called accessors. This enables data to be accessed easily and still helps promote the safety and flexibility of methods.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

class Myclass
{
    float seconds;

    // Declare a Code property of type string:
    public float Hours
    {
        get
        {
            return seconds / 3600.0f;
        }
        set
        {
            if (value < 0 || value > 24)
                throw new ArgumentOutOfRangeException(
                      $"{nameof(value)} must be between 0 and 24.");

            seconds = value * 3600;
        }
    }
}

In some cases, property get and set only return a value or assign a value, so the properties can be used auto-implemented to write. Note the code below only has the properties but no actual private field set. The required field of class of this kind of code will be set automatically during the compile.

1
2
3
4
5
6

public class SaleItem
{
   public string Name { get; set; }

   public int Price { get; set; }
}

The properties can also use body expression to simplify. Here we need to use the operator of =>. It could link a member with an expression. Here we don’t need to write the keywords of return but still require an private field.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

public class SaleItem
{
    string _name;
    decimal _cost;

    public string Name
    {
        get => _name;
        set => _name = value;
    }

    public decimal Price
    {
        get => _cost;
        set
        {
            if (value >= 0)
            {
                _cost = value;
            }
        }

    }
}

The abstract class may have an abstract property, which can be implemented in the derived class

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

public abstract class Person {
    public abstract string Name {
        get;
        set;
    }
}

class Student : Person {
    private string name = "N.A";
    private int age = 0;

    // Declare a Name property of type string:
    public override string Name {
        get {
            return name;
        }
        set {
            name = value;
        }
    }
}

Serialization and Deserialization

It is the process of converting an object into a stream of bytes to store the object or transmit it to memory. The stream of bytes can be deserialized to the object.

To serialize an object, the object should be have a SerializableAttribute attribute. Fields within a class that don’t need to be serialized should include a NonSerializedAttribute attribute.

Users can use binary or XML serialization to serialize an object. Below is a sample to use basic serialization to serialize a class.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

using System;
using System.IO;
using System.Runtime.Serialization;
using System.Runtime.Serialization.Formatters.Binary;

namespace testCSharp
{

    [Serializable]
    class TestSerialize
    {
        public int ID = 13;
        public string content = "test";

        [NonSerialized]
        public string content2 = "Costum";

        public int function()
        {
            return 0;
        }
    }

    class Program
    {
        static void Main(string[] args)
        {
            TestSerialize test1 = new TestSerialize();
            test1.ID = 1234;
            test1.content = "Hello World";
            test1.content2 = "Hello World 2";
            IFormatter formatter = new BinaryFormatter();
            Stream fs = new FileStream("data.txt", FileMode.Create, FileAccess.Write);

            formatter.Serialize(fs, test1);
            fs.Close();

            fs = new FileStream("data.txt", FileMode.Open, FileAccess.Read);
            TestSerialize test2 = (TestSerialize)formatter.Deserialize(fs);

            Console.WriteLine(test2.ID);    // 1234
            Console.WriteLine(test2.content);   // Hello World
            Console.WriteLine(test2.content2); // None
        }
    }
}

Thread

One thread if one execution flow for the code. For some parallel work in the same program, we can use multi-thread to save the total execution time.

See here for more information.

LINQ (Language Integrated Query)

Query expression is like the SQL language, it can search elements with some relationship. It starts with from and ends with select or group.

LINQ is the data object language that integrated into C#. It can be used for search, order, compare and summarize action.

1
2
3
4
5
6
7
8
9
10
11
12
13
14

List<User> users = new List<User>
{
    new User{Name = "a", Age = 27},
    new User{Name = "b", Age = 32},
    new User{Name = "c", Age = 15}
}
Enumerable<Uesr> selectUsers = from user in users
            where user.Age < 30
            orderby user.Age descending
            select user;

// Below is also work
var selectUsers = users.Where(user => user.Age < 30)
    .OrderByDescending(user => user.Age).Select(user => user);

LINQ can be used in following scenarios.

• Objects: object’s in code. e.g. class, collectiosn
• XML: XML file
• SQL: SQL database
• Entities
• Datasets

The structure of computer is simple. For hardware, computer includes Memory, Controller, Processor and I/O devices. For software, the basic element is operating system.

CPU

Central Processing Unit (CPU) is the brain of the computer. It receives data, execute commands and process the data.

CPU can also be divided into following parts according to their functions.

All parts above are connected together via electricity’s signal.

The working pipeline of CPU is as follows.

1. Fetch command. The Controller fetches the command from memory to registers, Program Counter stores the next address of command that needs to be executed.
2. Decoding command. The Controller decodes the command according to existed rules, recognizes operation category and the methods.
3. Executed command. The Controller handles the action of the command. e.g. Add numbers stored in two registers, compare two numbers.
4. Fetch data. If the command needs to handle data, the Controller will fetch the data from the memory according to the address decoded from the command.
5. Write Back. Write the answer of command to somewhere such as the registers in CPU.

Register

There are several kinds of register in CPU.

• There is only one Program Counter, Flag Register, Accumulation Register, Instruction Register, and Stack Register in CPU.
• There are several Base Register, Index Registers, and General Register in CPU.

Program Counter

It store the address of the unit in memory which stores the command that needs to be executed. It control the process of the program to be executed.

When the program is executed, the process is as follows.

1. The controller fetches the command from memory according to the the address that is stored in Program Counter
2. The controller analyzes and processes that command
3. The address in Program Counter will increase by 1 or change to the address according to the conditional/loop command(JMP command in Assembly language), which points to the unit which stores the next command.
4. If there is a function that needs to be executed, the next command will be stored in a Stack in memory, when the function is finished, the content of Program Counter will be set to the address in the top of Stack.

Flag Register

Flag Register stores the sign(+/-/0) of the Accumulation Register.

There is a compare action when conditional/loop function appears. When the compare function is executed, subtraction action will happen, and the answer is store in the Flag Register, then the Program Counter will be updated to corresponding address.

Base and Index Registers

A base register and several index registers can form an array. The array is stored continuously.

Memory

Memory has tight relationship with with CPU, CPU will fetch the command and data from disk to memory, and write back the command and data to disk.

There is several kinds of memory.

Memory has power, address signal, data signal, control signal.

I/O devices

Disk

The program stored in disk must be loaded to memory to be executed.

The disk has the following parts

Physcially, the disk is divided into different sector, which is the unit to do the read and write actions to disk. A disk will include 512 byte normally.

Operate System

Operate system could get over the difference of computer hardware except CPU.

The program just needs to call the API(Application Programming Interface) in operate system, then operate could handle the I/O devices.

Operate system includes:

• Control program. Includes the hardware control and program execution control
• Programming language processor. Compilation.
• Application. e.g. txt Editor

Reference

[1] WeChat article