General Mathematic Basis for SLAM
This post talks about the fundamental math for SLAM, including Homogeneous Coordinates, Transformation in 3D space, Probability, SVD, Least Square Optimization, Lie Group and Lie Algebra and etc.
Homogeneous Coordinate
- Convert from Euclidean coordinate to Homogeneous coordinate
- For point: append an extra dimension with value 1
- For vector (point at infinity): append an extra dimension with value 0
- Convert from Homogeneous coordinate to Euclidean coordinate
- For point: divide other dimensions by the last dimensions and then drop the last dimension
- For vector (point at infinity): drop the last dimension
For point
$$
\begin{bmatrix}
1 \\
2 \\
3
\end{bmatrix} \rightarrow
\begin{bmatrix}
1 \\
2 \\
3 \\
1
\end{bmatrix} =
\begin{bmatrix}
2 \\
3 \\
6 \\
2
\end{bmatrix}
$$
For lines and planes, use the vector formed by coefficient of the line / plane equation to represent. e.g. line $3x + 4y + 5z + 6 = 0$ represented by $[3, 4, 5, 6]^T$.
More properties
- One coordinate multiplied by a non-zero scalar still represents the same point, e.g. $[2, 4, 1]^T = [4, 8, 2]^T$. This is also the definition of homogeneous coordinate
- Square sum of all dimensions cannot equal to 0. This is also the definition
- Setting last dimension to 0 could represent the point in infinitely far away, e.g. $[2, 4, 0]^T$. Even the point is far away, the direction information is still represented
- Setting dimensions except the last dimension to 0 could represent the line / plane in infinitely far away (horizon line), e.g. $[0, 0, 1]$ for line, $[0, 0, 0, 1]$ for plane.
- Dot production of 0 between line/plane and point coordinate means the point is inside the line/plane. $l \cdot x = l^T x = 0$
- Cross proudction between 2 lines or 2 planes could get the intersections $x = l_1 \times l_2$; Cross production between 2 points could get the line between the two points $l = x_1 \times x_2$
Coordinate Transformation: 3D Pose Representation
In 3D space, every object could be represented by a reference frame attached to it. There are 2 main reference frames.
- World reference frame $O_w$. Stationary. Usually chosen as the initial camera reference frame
- Camera reference frame $O_c$. Attached to camera, moving with camera.
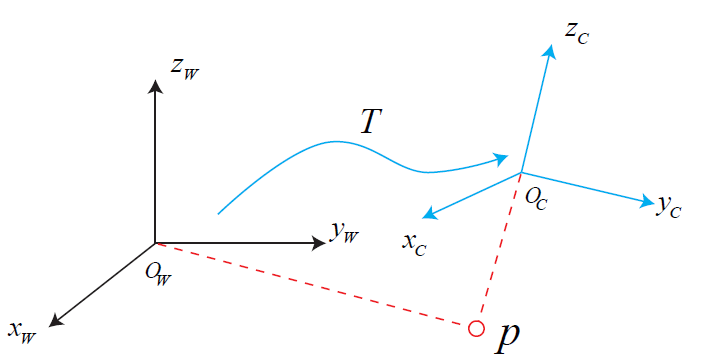
Then we can describe the camera pose inside the world reference frame using coordinate values under world reference frame.
- 3DoF Position: $t_{wc} \in \mathbb{R}^3$, the vector from world origin to camera origin, and is under world reference frame
- 3DoF Orientation: $R_{wc} \in \mathbb{R}^{3\times3}$, rotation matrix, columns are camera frame’s $x$, $y$, $z$ axle under world reference frame
- or quaternion $\mathbb{R}^4$, or euler angles $\mathbb{R}^3$, or axis-angle $\mathbb{R}^4$
Transformation matrix
By combing the position and orientation, we could get
$$
\begin{aligned}
\mathrm{SE(3)} &= \left\lbrace
T = \begin{bmatrix}
R & t \\
0^T & 1
\end{bmatrix}
\in \mathbb{R}^{4\times4} |
R \in \mathrm{SO(3)}, t \in \mathbb{R}^3
\right\rbrace \\
\mathrm{SO(3)} &= \lbrace R \in \mathbb{R}^{3\times3}|RR^T = I, \det( R )=1 \rbrace
\end{aligned}
$$
Specifically, we have
$$
T_{wc} = \begin{bmatrix}
R_{wc} & t_{wc} \\
0^T & 1
\end{bmatrix}
$$
The transformation matrix $T_{wc}$ could express different physical meanings as following.
$T_{wc}$ represents to transform the homogeneous coordinate of points / vectors from camera reference frame $O_c$ to world reference $O_w$.
For a space point $p$, there is
$$
\mathbf{p}_w = T_{wc} \mathbf{p}_c =
\begin{bmatrix}
\ R_{wc}p_c + t_{wc} \\
1
\end{bmatrix}$$
where
- $p_c$: coordinate of point p in camera reference frame $O_c$
- $\mathbf{p}_c$: homogeneous coordinate of point p in camera reference frame $O_c$
- $\mathbf{p}_w$: homogeneous coordinate of point p in world reference frame $O_w$
- $T_{wc}$: transformation of world frame from camera frame
- $R_{wc}$: column vectors are the coordinate of camera’s axe in world frame
- $t_{wc}$: vector from world origin to camera origin, and expressed under world frame
Note. $\mathbf{p}_c$ and $\mathbf{p}_w$ are different because the reference frame they expressed change, while the physical position of $p$ doesn’t change.
For a vector $v$, there is
$$
\mathbf{v}_w = T_{wc} \mathbf{v}_c =
\begin{bmatrix}
\ R_{wc}v_c \\
0
\end{bmatrix}$$
The difference is the homogeneous coordinate for a vector is to append $0$ in the end
$t_{wc}$
- Coordinate of camera origin in world frame $O_w$
- Vector from world origin to camera origin and under world frame $O_w$
$$
\mathbf{p}_w = T_{wc} \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix} = \begin{bmatrix}
\ t_{wc} \\
1
\end{bmatrix}
$$
$R_{wc}$
- Columns are camera’s axes in world frame $O_w$
- Rows are world’s axes in camera frame $O_c$
$$
\mathbf{v}_w^{(1)} = T_{wc} \begin{bmatrix}
1 \\
0 \\
0 \\
0 \\
\end{bmatrix}
=
\begin{bmatrix}
R_{wc}^{(2)} \\
0
\end{bmatrix},
\mathbf{v}_w^{(2)} = T_{wc} \begin{bmatrix}
0 \\
1 \\
0 \\
0 \\
\end{bmatrix}
=
\begin{bmatrix}
R_{wc}^{(2)} \\
0
\end{bmatrix},
\mathbf{v}_w^{(3)} = T_{wc} \begin{bmatrix}
0 \\
0 \\
1 \\
0 \\
\end{bmatrix}
=
\begin{bmatrix}
R_{wc}^{(3)} \\
0
\end{bmatrix}
$$
$T_{wc}$ could represent as a transformation operator to “move” the camera frame from world frame origin to where the camera frame is.
The columns of $R_{wc}$ could be constructed by angle $\theta_{cw}$, which is to rotate the reference frame from world frame origin to camera frame.
Also the $t_{wc}$ can also represent to translate the camera frame from the world origin’s position to camera origin’s position
Note. This is to operate the reference frame itself, it has the “reversed” meaning from transforming the coordinate of point between reference frames, where the reference frames are not moved.
$T_{wc}$ and $T_{cw}$
Since the transformation between reference frame is bi-directional. $T_{cw}$ could also be used to describe camera pose.
- $T_{cw} = T_{wc}^{-1}$: the coordinate transformation of camera frame $O_c$ from world frame $O_w$
- $R_{cw} = R_{wc}^{-1}$: column vector is the coordinate of world axes in camera frame
- $t_{cw} = -R_{wc}^{-1}t_{wc}$: vector from camera origin to world origin, and expressed under camera frame
The camera pose $T_{wc}$ or $T_{cw}$ is also called extrinsic, and it could also be transferred to a $\mathbb{R}^6$ vector using Lie Algebra.
Since both $T_{wc}$ and $T_{cw}$ could represent camera pose, we usually use the expressions of coordinate transformations and avoid to use the ambiguity term “camera pose”.
- The transformation of world frame from camera frame ($T_{wc}$)
- The transformation of camera frame from world frame ($T_{cw}$)
RANSAC (Random Sample Consensus)
- A method to eliminating the outlier data (seperate data into inliners and outliers). Steps are
- Sample the number of data required to fit the model
- Compute model using the sampled data points
- Score the model by the fraction of inliers within a preset threshold of the model
- Repeat the above steps until the best model is found
- Repeat Times $T$ of RANSAC to find the best model
$$
T = \frac{\log(1-p)}{\log(1-w^n)}
$$
where $p$ is the desired probability to find the best model, $w$ is the fraction of number of inliner to the number of whole data, and $n$ is the number of fit the model. - Properties
- The large $p$ or $n$, the more times required to perform RANSAC
- The large $w$, the less times required to perform RANSAC
- Good for model required little data points to fit
Linear Equations
Set matrix $A \in \mathbb{R}^{m\times n}$, where $rank(A) = \min(m, n)$, vector $x \in \mathbb{R}^n$, vector $b \in \mathbb{R}^m$.
Linear homogeneous equations
$$
A x = \mathbf{0} \quad \begin{cases}
\begin{aligned}
m < n, \quad &\text{use Gaussian elimination} \\
&x = \sum_{i=0}^{n-m} \lambda_i \xi_i
\end{aligned} \\
m = n, \quad \text{only have solution}, \quad x = 0 \\
\begin{aligned}
m > n, \quad &\text{convert to least square problem} \\
&x^\star = \arg\min\limits_x ||Ax|| \ s.t. \ ||x|| = 1
\end{aligned}
\end{cases}
$$
Solutions to solve least square problem of overdetermined equations.
Method 1: EVD of $A^TA$
$x^\star$ is the eigen vector respective to the least eigen value of $A^TA$
Proof
Convert optimization problem with constraints to non-constraints
$$
\begin{aligned}
&\min_x ||Ax|| \ s.t. \ ||x|| = 1 \\
\Rightarrow& \min_x (x^TA^TAx + \lambda (1-x^Tx))
\end{aligned}
$$
Compute the derivative of target function on $x$
$$
\frac{\mathrm{d} (x^TA^TAx + \lambda (1-x^Tx))}{\mathrm{d} x} = 2A^TAx - 2\lambda x \in \mathbf{R}^n
$$
The result $x^*$ is to make the derivative equals to 0, thus
$$
A^TAx^* = \lambda x^\star
$$
which means $x^\star$ is the eigen vector of $A^TA$, $\lambda$ is the eigen value of $A^TA$.
Bring back to the optimization problem
$$
\begin{aligned}
&\min_x (x^TA^TAx + \lambda (1-x^Tx)) \\
\Rightarrow& \min_x (x^T \lambda x) = \lambda
\end{aligned}
$$
Therefore, the minimal of optimization target is the least eigen value of matrix $A^TA$, and $x^\star$ is the respective eigen vector.
Method 2: SVD of $A$
$x^\star$ is the last column of matrix $V$, which is the SVD of $A=U\Sigma V^T$. See SVD section for more details
Linear non-homogeneous equations
$$
A x = \mathbf{b} \quad \begin{cases}
\begin{aligned}
m < n, \quad &\text{use Gaussian elimination} \\
&x^\star = x_0 + \sum_{i=0}^{n-m} \lambda_i \xi_i
\end{aligned} \\
m = n, \quad x^\star = A^{-1}b \\
\begin{aligned}
m > n, \quad &\text{convert to least square problem} \\
&x^\star = \arg\min_x ||Ax - \mathbf{b}||
\end{aligned}
\end{cases}
$$
Note. If $rank(A|b) < rank(A)$, there is no solution, but could still convert to least square problem to get a approximated result.
Solutions to solve least square problem of overdetermined equations.
Method 1: Inverse of $A^TA$
$x^\star = (A^T A)^{-1}A^T\mathbf{b}$
Proof
Since
$$
||Ax - \mathbf{b}|| = x^TA^TAx - 2\mathbf{b}^T Ax + \mathbf{b}^T \mathbf{b}
$$
Then
$$
\frac{\mathrm{d} ||Ax - \mathbf{b}||}{\mathrm{d} x} = 2A^TAx - 2A^T \mathbf{b} \in \mathbb{R}^{n}
$$
To get the $x^\star$ which makes optimization target reaches minimal, we set its derivative to $\mathbf{0}$. (This cannot be the $x$ making optimization target reaches maximum value because the maximum value is infinity)
$$
x^\star = (A^TA)^{-1} A^T \mathbf{b}
$$
If applying SVD for matrix $A$, we could get
$$
x^\star = (V \Sigma^T U U \Sigma V^T)^{-1} V \Sigma^T U^T \mathbf{b} = V \Sigma^{-1} U^T \mathbf{b}
$$
Method 2: SVD of $A$
See SVD section for more details.
Matrix Decomposition
LU
Lower-upper Decomposition for square matrix $A_{n\times n}$ with $rank(A) = n$, to a lower triangle matrix and a upper triangle matrix.
$$
A = LU = \begin{bmatrix}
1 & 0 & \cdots & 0 \\
\star & 1 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
\star & \star & \cdots & 1
\end{bmatrix}
\begin{bmatrix}
\star & \star & \cdots & \star \\
0 & \star & \cdots & \star \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & \star
\end{bmatrix}
$$
The matrix $U$ is the result to use Gaussian elimination, and $[A | I] \rightarrow [U | L^{-1}]$
Usages
converting to
$$
\begin{cases}
Ly = \mathbf{b} \\
Ux = y
\end{cases}
$$
Although the LU decomposition still requires Gaussian elimination, this is very helpful if the $\mathbf{b}$ keep changing.
Extension: LUP decomposition for non-square matrix, $P_{n\times m}A_{m\times n} = LU$
converting to
$$
\begin{cases}
Ly = P\mathbf{b} \\
Ux = y
\end{cases}
$$
Cholesky
A special LU decomposition for real symmetric positive definite matrix $A_{n\times n} = A^T$, where L is lower triangle matrix
$$
A = L L^T
$$
Usages
solve $Ax = \mathbf{b}$
converting to
$$
\begin{cases}
Ly = \mathbf{b} \\
L^T x = y
\end{cases}
$$
QR
QR Decomposition for matrix $A_{m \times n}$, and $m \geq n$, to a orthogonal matrix $Q$ and a upper triangle matrix $R$.
$$
A = Q_{m \times m} \begin{bmatrix}
R_{n \times n} \\
0_{(m - n) \times n}
\end{bmatrix}
$$
Use Gram-Schmidt to convert matrix $A = [a_1, \cdots, a_n]$ to orthogonal vectors $[q_1, \cdots, q_n] = A T$, where matrix $T$ is an upper triangle matrix, and its inverse is matrix $R$, which is still an upper triangle matrix.
Usages
$$A_{m\times n} = Q_{m\times n}R_{n\times n} \rightarrow Q^TAQ = RQ$$
Let $A_2 = RQ$, whose eigenvectors are same with $A$. Repeat the QR decomposition, until the $A_n$ is a diagonal matrix.
$$
\begin{split}
x^\star &= (A^T A)^{-1}A^T\mathbf{b} = (R^TQ^TQR)^{-1}R^TQ^T\mathbf{b} \\
&=(R^TR)^{-1}R^TQ^T\mathbf{b} \\
&=R^{-1}Q^T\mathbf{b}
\end{split}
$$
EVD
Eigenvalue Decomposition for square matrix $A_{n\times n}$
$$
A V = V \Sigma
$$
where $V = [v_1, v_2, \cdots, v_n]$ and $v_i$ is the eigenvector, and $\Sigma = diag(\lambda_1, \lambda_2, \cdots, \lambda_n)$ is the eigenvalue. So
$$
A = V \Sigma V^{-1}
$$
Usages
$A \approx V_{n\times r} \Sigma_{r\times r} V_{n\times r}^{-1}$
converting to
$$
\begin{cases}
V y = b \\
\Sigma z = y \\
V^{-1} x = z
\end{cases}
$$
SVD
Singular Value Decomposition is a useful method to solve equations or estimate a matrix, so we put it into a separate section.
If we have a matrix $A$ with size $m\times n$, we could have its SVD like
$$
A = U \Sigma V^T
$$
where
| Element | Size | Meaning |
|---|---|---|
| $U$ | $m \times m$ | formed by eigenvectors of $A A^T$ |
| $\Sigma$ | $m \times n$ | diagonal matrix where values are singular value, $\sigma_i = \sqrt{\lambda_i}$, and $\lambda_i$ are the eigen values of $A A^T$ and $A^T A$ |
| $V$ | $n \times n$ | formed by eigenvectors of $A^T A$ |
Besides, we have $U^T = U^{-1}$ and $V^T = V^{-1}$ because $A A^T$ and $A^T A$ are symmetric matrix
Usages
$A \approx U_{m \times r} \Sigma_{r \times r} V_{r \times n}^T$
Target
$$
\min_x || Ax || \quad s.t. \quad || x || = 1
$$
where $A \in \mathbb{R}^{m\times n}$, and $m > n$, which means there are more observations than unknown
$$
\begin{split}
&\min_x || Ax || = \min_x || U\Sigma V^T x || \\
=& \min_x || \Sigma V^T x || \\
=& \min_y || \Sigma y || = \min_y y^T \Sigma^T \Sigma y \\
=& \min_y \Sigma_{i=0}^k y_i^2 \sigma_i^2 \quad s.t. \quad ||y|| = 1
\end{split}
$$
Explanation
If a matrix $B^T = B^{-1}$, then
$$
|| Bx || = x^T B^T B x = x^T x = || x ||
$$
For vector $y$, we also have $|| y || = 1$. The reason is because
$$
V^T x = \begin{bmatrix}
e_1^T \\
e_2^T
\end{bmatrix} x = \begin{bmatrix}
e_1^T x \\
e_2^T x
\end{bmatrix} = \begin{bmatrix}
\cos (\theta) \\
\cos (\frac{\pi}{2} - \theta)
\end{bmatrix}
$$
where $\theta$ is the angle between unit vector $e_1$ and $x$
Therefore, when the $y^* = [0, 0, \cdots, 1]^T$, then $\min || Ax || = \sigma_k^2$
Then $x^* = (V^T)^{-1} y^* = V [0, 0, \cdots, 1]^T$, which means $x^*$ is the last column of matrix $V$.
Target
$$
\min_x || Ax - \mathbf{b}||
$$
where $A \in \mathbb{R}^{m\times n}$, and $m > n$, which means there are more observations than unknown
$$
\begin{split}
&\min_x || Ax - \mathbf{b}|| = \min_x || U\Sigma V^T x - \mathbf{b} || \\
=& \min_x || \Sigma V^T x - U^T \mathbf{b} || \\
=& \min_y || \Sigma y - \mathbf{b}^{\prime} ||
\end{split}
$$
Then $y^\star = \Sigma^{-1} \mathbf{b}^\prime = [\frac{\mathbf{b}^{\prime}_0}{\sigma_0}, \cdots, \frac{\mathbf{b}^{\prime}_n}{\sigma_n}]^T = V^Tx^\star$
And $x^\star = Vy^\star = V\Sigma^{-1}\mathbf{b}^\prime = V \Sigma^{-1} U^Tb$
Derivative of Matrix (Jacobian Matrix)
$x = [x_1, \cdots, x_n]^T \in \mathbb{R}^n $
Scalar on Vector
$f(x) \in \mathbb{R}$
$$
\frac{\mathrm{d}f}{\mathrm{d}x} = \left[ \frac{\mathrm{d}f}{\mathrm{d}x_1}, \cdots, \frac{\mathrm{d}f}{\mathrm{d}x_n} \right]^T \in \mathbb{R}^n
$$
or
$$
\frac{\mathrm{d}f}{\mathrm{d}x^T} = \left[ \frac{\mathrm{d}f}{\mathrm{d}x_1}, \cdots, \frac{\mathrm{d}f}{\mathrm{d}x_m} \right] \in \mathbb{R}^{1 \times n}
$$
Specifically, if $b\in\mathbb{R}^n$
$$
\frac{\mathrm{d} (b^Tx)}{\mathrm{d} x} = b \in \mathbb{R}^n
$$
Vector on Vector
$F(x) = [f_1(x), \cdots, f_m(x)]^T \in \mathbb{R}^m$
$$
\frac{\partial F}{\partial x^T} = \begin{bmatrix}
\frac{\partial f_1}{\partial x^T} \\
\vdots \\
\frac{\partial f_m}{\partial x^T}
\end{bmatrix} = \begin{bmatrix}
\frac{\mathrm{d}f_1}{\mathrm{d}x_1} & \cdots & \frac{\mathrm{d}f_1}{\mathrm{d}x_n} \\
\vdots & \ddots & \vdots \\
\frac{\mathrm{d}f_m}{\mathrm{d}x_1} & \cdots & \frac{\mathrm{d}f_m}{\mathrm{d}x_n}
\end{bmatrix}
\in \mathbb{R}^{m \times n}
$$
Specifically, if $A\in\mathbb{R}^{m\times n}$
$$
\frac{\mathrm{d} (Ax)}{\mathrm{d} x^T} = A \in \mathbb{R}^{m\times n}
$$
Lie Group and Lie Algebra
- Group: $G = (A, \cdot)$
- Lie Group: continuous group
- Lie Algebra: $(V, F, [])$
$SO(3)$ and $so(3)$
$$
SO(3) = \lbrace R \in \mathbb{R}^{3\times3}|RR^T = I, det( R )=1 \rbrace
$$
For $R_1 \in SO(3)$ and $R_2 \in SO(3)$, $R_1 R_2 \in SO(3)$
Lie Algebra $so(3)$
$$
so(3) = \lbrace \phi \in \mathbb{R}^3, \Phi=\phi^{\wedge} \in \mathbb{R}^{3\times3} \rbrace
$$
For $\phi_1 \in so(3)$ and $\phi_2 \in so(3)$, $[\phi_1, \phi_2] = [ \Phi_1\Phi_2 - \Phi_2\Phi_1 ]^{\vee} \in so(3)$
Convert $SO(3) \Leftrightarrow so(3)$
For respective $R \in SO(3)$ and $\phi \in so(3)$
$$
\begin{split}
R &= \exp(\phi^{\wedge}) = \sum_{n=0}^{\infty}\frac{(\phi^{\wedge})^n}{n!} \\
&= \cos\theta I + (1 - \cos\theta) aa^T + \sin\theta a^{\wedge}
\end{split}
$$
where $\phi = \theta a$, a is a vector with $||a|| = 1$.
$$
\begin{aligned}
a^{\wedge}a^{\wedge} = aa^T - I \\
a^{\wedge}a^{\wedge}a^{\wedge} = -a^{\wedge}
\end{aligned}
$$
$$
\begin{split}
\phi &= \ln(R)^{\vee} = (\sum_{n=0}^{\infty} \frac{(-1)^n}{n+1} (R+I)^{n+1})^{\vee} \\
&= \theta a =
\begin{cases}
\theta = \arccos\frac{tr(R) - 1}{2} \\
\text{solve} \ a \ \text{by} \ Ra = a
\end{cases}
\end{split}
$$
$SE(3)$ and $se(3)$
$$
SE(3) = \left\lbrace T =
\begin{bmatrix}
R & t \\
0 & 1
\end{bmatrix}
\in \mathbb{R}^{4\times4}|R \in SO(3), t \in \mathbb{R}^{3}
\right\rbrace
$$
For $T_1 \in SE(3)$ and $T_2 \in SE(3)$, $T_1 T_2 \in SE(3)$
$$
se(3) = \left\lbrace \xi =
\begin{bmatrix}
\rho \\
\phi
\end{bmatrix} |
\rho \in \mathbb{R}^{3}, \phi \in SO(3)
\right\rbrace
$$
For $\xi_1 \in se(3)$ and $\xi_2 \in se(3)$, $[\xi_1, \xi_2] = [ \xi_1^{\wedge}\xi_2^{\wedge} - \xi_2^{\wedge}\xi_1^{\wedge} ]^{\vee} \in se(3)$
$$
\xi^{\wedge} =
\begin{bmatrix}
\phi^{\wedge} & \rho \\
0^T & 0
\end{bmatrix}
\in
\mathbb{R}^{4 \times 4}
$$
Convert $SE(3) \Leftrightarrow se(3)$
For respective $T \in SE(3)$ and $\xi \in se(3)$
$$
\begin{split}
T &= \exp(\xi^{\wedge}) = \sum_{n=0}^{\infty}\frac{(\xi^{\wedge})^n}{n!} \\
&= \begin{bmatrix}
\exp(\phi^{\wedge}) & J\rho \\
0^T & 1
\end{bmatrix}
\end{split}
$$
where
$$
J = \frac{\sin\theta}{\theta} I + \left( 1 - \frac{\sin\theta}{\theta} \right) aa^T + \frac{1 - \cos\theta}{\theta} a^{\wedge}, \ \phi = \theta a
$$
$$
\xi = \begin{bmatrix}
\rho \\
\phi
\end{bmatrix} =
\begin{cases}
\theta = \arccos\frac{tr(R) - 1}{2} \\
\text{solve} \ a \ \text{by} \ Ra = a \\
t = J\rho
\end{cases}
$$
Derivative of Lie Algebra
Derivative of $so(3)$
The derivative of $\frac{\partial Rp}{R}$ is hard to calculate because the $SO(3)$ have constraint and cannot do addition, where $R \in SO(3)$ is rotation matrix, $p \in \mathbb{R}^{3}$ is a point in space. But we can calculate the derivative of respective Lee Algebra $\phi$.
$$
\begin{split}
\frac{\partial \exp(\phi^{\wedge})p}{\partial \phi^T}
&= \lim_{\delta\phi \rightarrow 0} \frac{\exp((\delta\phi)^{\wedge})\exp(\phi^{\wedge})p - \exp(\phi^{\wedge})p}{\delta\phi^T} \\
&= \lim_{\delta\phi \rightarrow 0} \frac{(I + (\delta\phi)^{\wedge})\exp(\phi^{\wedge})p - \exp(\phi^{\wedge})p}{\delta\phi^T} \\
&= \lim_{\delta\phi \rightarrow 0} \frac{(\delta\phi)^{\wedge}\exp(\phi^{\wedge})p}{\delta\phi^T} \\
&= \lim_{\delta\phi \rightarrow 0} \frac{-(\exp(\phi^{\wedge})p)^{\wedge}\delta\phi}{\delta\phi^T} \\
&= -(\exp(\phi^{\wedge})p)^{\wedge} \\
&= -(Rp)^{\wedge} \in \mathbb{R}^{3\times 3}
\end{split}
$$
For the derivative on point $p$
$$
\begin{split}
\frac{\partial \exp(\phi^{\wedge})p}{\partial p^T} = p
\end{split}
$$
Derivative of $se(3)$
Similarily, the derivative to $T \in SE(3)$ can also be finished in Lee Algebra $\xi \in se(3)$, and point in homogeneous coordiante $\mathbf{p} = [x \ y \ z \ 1]^T = [p^T \ 1]^T$
$$
\begin{split}
\frac{\partial \exp(\xi^{\wedge})\mathbf{p}}{\partial \xi^T}
&= \lim_{\delta\xi \rightarrow 0} \frac{\exp((\delta\xi)^{\wedge})\exp(\xi^{\wedge})\mathbf{p} - \exp(\xi^{\wedge})\mathbf{p}}{\delta\xi^T} \\
&= \lim_{\delta\xi \rightarrow 0} \frac{(I + (\delta\xi)^{\wedge})\exp(\xi^{\wedge})\mathbf{p} - \exp(\xi^{\wedge})\mathbf{p}}{\delta\xi^T} \\
&= \lim_{\delta\xi \rightarrow 0} \frac{(\delta\xi)^{\wedge}\exp(\xi^{\wedge})\mathbf{p}}{\delta\xi^T} \\
&= \lim_{\delta\xi \rightarrow 0} \frac{\begin{bmatrix}
(\delta\phi)^{\wedge} & \delta\rho \\
0^T & 0
\end{bmatrix}
\begin{bmatrix}
Rp + t \\
1
\end{bmatrix}}{\delta\xi^T} \\
&= \lim_{\delta\xi \rightarrow 0} \frac{\begin{bmatrix}
(\delta\phi)^{\wedge}(Rp + t) + \delta\rho \\
0^T
\end{bmatrix}}{[\delta\rho^T \quad \delta\phi^T]} \\
&= \begin{bmatrix}
I_{33} & -(Rp+t)^{\wedge} \\
0^T & 0^T
\end{bmatrix} \in \mathbb{R}^{4\times 6}
\end{split}
$$
The result is a $4\times 6$ matrix, and the $R, t$ can be extracted from $T \in SE(3)$, which can be calculated from $\xi \in se(3)$ by $\exp(\xi^{\wedge})$.
If we drop the last row, we can get
$$
\frac{\partial (Rp + t)}{\partial \xi^T} = \begin{bmatrix}
I_{33} & -(Rp+t)^{\wedge}
\end{bmatrix}
$$
For the derivative on point $p$
$$
\frac{\partial \exp(\xi^{\wedge})\mathbf{p}}{\partial p^T} = \frac{\partial (Rp + t)}{\partial p^T} = R
$$
Probability Theory
- Probability
- Marginalization
- Indenpence / Conditional Indenpence
- Bayes Rules
$$ P(x|y) = \frac{P(y|x)P(x)}{P(y)} $$- Joint Probability $P(x|y)$
- Likelihood Probability $P(y|x)$, prior probability $P(x)$
- Background Knowledge $z$ besides $x, y$
$$
P(x|y, z) = \frac{P(y|x, z) P(x|z)}{P(y | z)}
$$
- Normal (Gauss) Distribution
- 1-d, N-d
- The multivariate normal distribution of k-dimensional random vector $\mathbf{X}=(X_1, \cdots, X_k)^T$, which is $$\mathbf{X} \sim \mathcal{N}(\mu, \Sigma)$$
The distribution is
$$
f_{\mathbf{X}}(x_1, \cdots, x_k) = \frac{1}{((2\pi)^k |\Sigma|)^{1/2}} \exp\left( -\frac{1}{2} (\mathbf{x}-\mu)^T \Sigma^{-1} (\mathbf{x}-\mu) \right)
$$