SLAM Learning Resources

Posted on Edited on In ,

This post organizes the resources that I used to learn SLAM, also serves as a reference to other post in this blog.

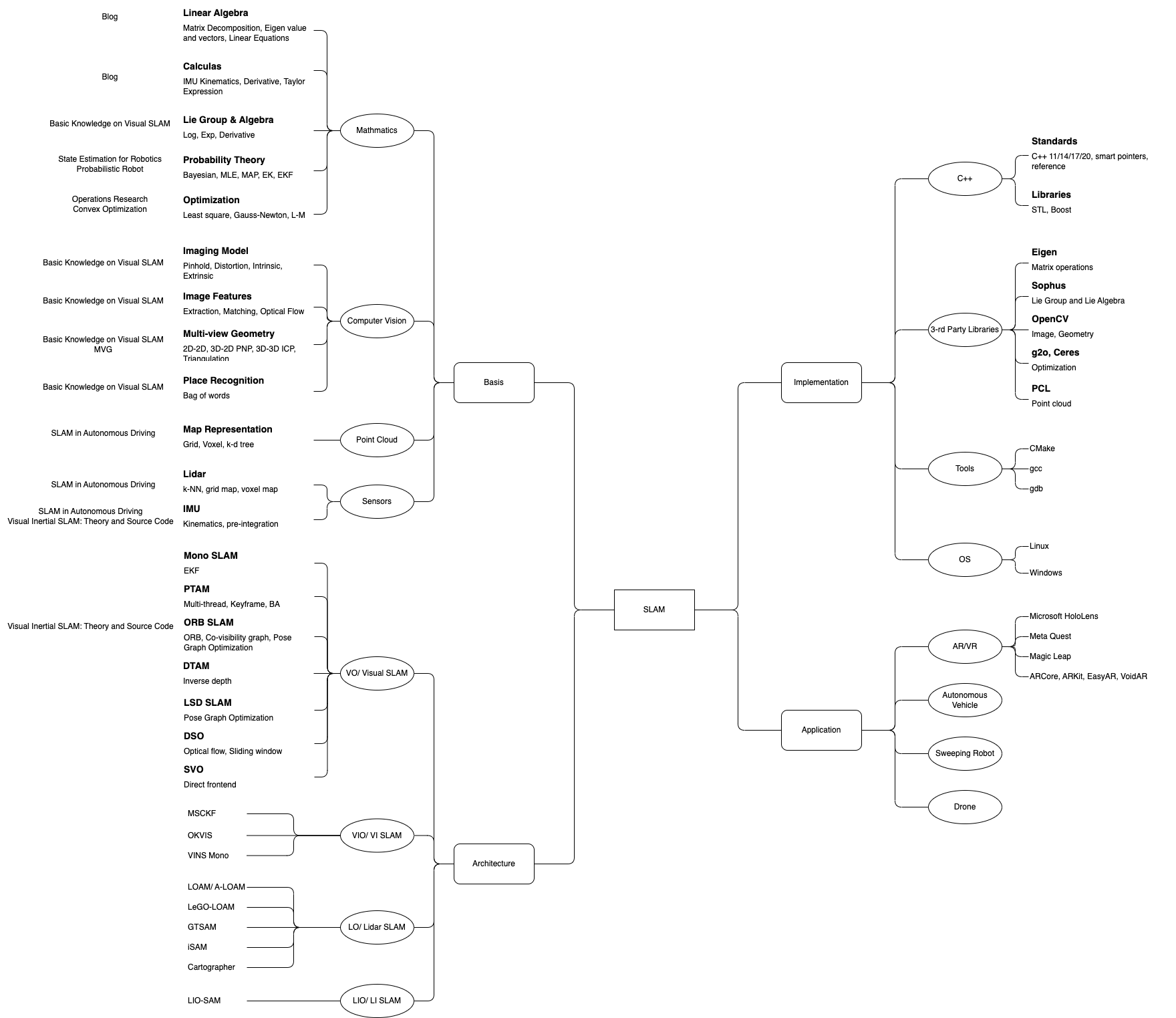
SLAM Knowledge Graph

Book

English Version Chinese Version Description
Basic Knowledge on Visual SLAM: From Theory to Practice 视觉SLAM十四讲 Visual SLAM architecture, including frontend, backend, loop closing detection, mapping, Lie Group and Lie Algebra and optimization
SLAM in Autonomous Driving book 自动驾驶中的SLAM技术 IMU Kinematics, pre-integration, ESKF, IEKF, GINS, LO, Loosely-coupled / Tightly-coupled LIO, High-fi map
Visual Inertial SLAM: Theory and Source Code 视觉惯性SLAM：理论与源码解析 SLAM engineering details based on ORB SLAM 2 & 3. VIO, multi-map theory
State Estimation for Robotics 机器人学的状态估计 SLAM backend mathematic theory. Recursive methods and batch estimations methods for MAP estimation. Lie Group and Lie Algebra for 3D space optimization
Multiple View Geometry in Computer Vision 计算机视图中的多视图几何 2D/3D Euclidean/Projective Transformations, Camera projection model, monocular, 2-view, 3-view and multi-view geometry
Convex Optimization 凸优化 Methods to analyze and solve optimization problem
OpenCV related books ~ Some books focus on the application of OpenCV like AR, SfM, Object Detection

Course

Course Name Description
Online Lectures: Basics for Robotics & Photogrammetric Computer Vision (Cyrill Stachniss, 2020) Introduces the 3d space movement and basic Mathematics theory used in SLAM like homogeneous coordinates, RANSAC
Online Course: Photogrammetric Computer Vision Block - Course Introduction (Cyrill Stachniss, 2020) Covers the details about different CV algorithm, including feature extraction and pose calculation from images
运筹学相关课程 Covers lots of content, but could only focus on how to solve non-linear optimization problem for learning

Classic Paper

Related Paper

Blogs

Knowledge Index

Describe camera pose in space

  • Pose change matrix $T$
  • SO(3), SE(3), so(3), se(3)
  • Homogeneous coordinate
  • Different projection types
    • 3D - in homogeneous coordinate
      • Euclidean: rotation + translation, 6DoF
      • Similarity: rotation + translation + scale: 7DoF
      • Affine: 12DoF
      • Projective: 15DoF
    • 2D - in homogeneous coordinate
      • Rigid / Euclidean: rotation + translation, 3DoF
      • Linear: rotation + scale, 2DoF
      • Similarity: rotation + translation + scale, 4DoF
      • Affine: rotation + translation + scale + shear, 6DoF
      • Projective: 8DoF

Camera imaging model

  • Pinhole camera model
    • Focal length x, y, optical center, skew coefficient, all in pixels
    • Coordinate in camera frame, normalized imaging plane, pixel frame
  • Lens distortion
    • radial distortion, tangential distortion
  • Calibration - Zhang’s method

Frontend - Feature-based method

  • Feature extraction
    • Keypoints and descriptors
    • ORB feature (Oriented FAST and Steer BRIEF)
  • Feature matching
    • Brute force
    • FLANN (Fast library of approximate nearest neighbors)
    • Optical flow
      • Pixel patch
  • 2D-2D
    • Fundamental and essential matrix (vector in same plane)
      • 8 point pairs, 8 unknown
      • Singular value $(\sigma, \sigma, 0)^T$
      • Recover $R$ and $t$ from $E$
    • Homography matrix (pixels relationship assuming there are in same plane)
      • 4 point pairs, 8 unknown
    • Triangulation
  • 3D-2D
    • DLT
      • 6 point pairs, 12 unknown
    • P3P
      • 3 points + 1 point for validation
    • Bundle adjustment (similar to backend)
  • 3D-3D
    • ICP, SVD
    • Bundle adjustment (similar to backend)

Frontend - Direct method

  • Minimizing photometric error
  • Similar to backend optimization

Backend - Filter (MAP, Incremental)

  • Kalman filter
  • Extended Kalman filter

Backend - Optimization (Usually MLE, Batch)

  • Optimization target
    • Put poses and mappoints together as the state vector
    • Derivate of error term on pose
    • Derivate of error term on mappoint’s position

$$
\frac{\partial e_{ij}}{\partial \xi_i} = -\left[\begin{matrix}
\frac{f_x}{Z_j^{\prime}} & 0 & -\frac{f_x X_j^{\prime}}{(Z_j^{\prime})^2} & -\frac{f_x X_j^{\prime} Y_j^{\prime}}{(Z_j^{\prime})^2} & f_x+\frac{f_x(X_j^{\prime})^2}{(Z_j^{\prime})^2} & -\frac{f_x Y_j^{\prime}}{Z_j^{\prime}} \\
0 & \frac{f_y}{Z_j^{\prime}} & -\frac{f_y Y_j^{\prime}}{(Z_j^{\prime})^2} & -f_y - \frac{f_y(Y_j^{\prime})^2}{(Z_j^{\prime})^2} & \frac{f_y X_j^{\prime} Y_j^{\prime}}{(Z_j^{\prime})^2} & \frac{f_y X_j^{\prime}}{Z_j^{\prime}}
\end{matrix}\right]
$$

$$
\frac{\partial e_{ij}}{\partial p_j} = -\left[\begin{matrix}
\frac{f_x}{Z_j^{\prime}} & 0 & -\frac{f_x X_j^{\prime}}{(Z_j^{\prime})^2} \\
0 & \frac{f_y}{Z_j^{\prime}} & -\frac{f_y Y_j^{\prime}}{(Z_j^{\prime})^2}
\end{matrix}\right] R_i
$$

  • Solve delta element $\mathbf{H} \mathbf{\Delta x} + \mathbf{b} = 0$
    • Schur complement
  • Iterative solution
    • Gradient Descent - first derivate of $F(\mathbf{x})$
    • Newton - second derivate of $F(\mathbf{x})$
    • Gauss-Newton - first derivate of $f(\mathbf{x})$
    • Levengerg-Marquardt - combination of gradient descent and gauss-newton
  • Acceleration
    • Sliding window
    • Marginalization using Schur complement
    • Pose graph

Loop Closure

  • Use K-means to build the dictionary, which is a d level k-ary tree
  • Use vector to represent the words frequency appearing in the frame